Ein Projekt von Natalie Traxler
Lösung Grundaufgabe:
https://scratch.mit.edu/projects/492259970
Zum Zeichnen benötigst du die Erweiterung Malstift. Aktiviere diese links unten.
Nimm als Figur einen kleinen Punkt.
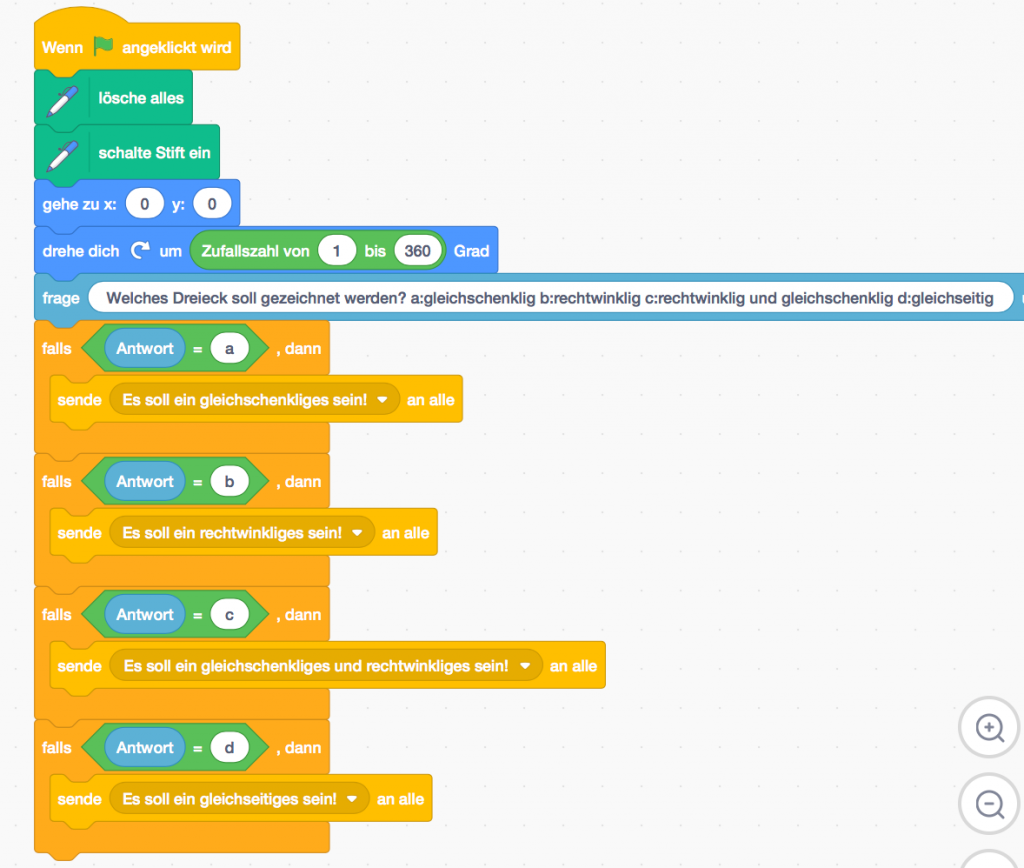
Wähle einen Startpunkt und gegebenenfalls Startrichtung.
Frage ab, welches Dreieck gezeichnet werden soll. Je nach Antwort wird ein anderer Code
für das jeweilige Dreieck gebraucht.
Dies kann gelöst werden durch die „falls (), dann“ Steuerung und das Senden von
Nachrichten, die jeweils als Startereignis für den jeweiligen Code genutzt werden. Durch
das Nutzen der Nachrichten wird der gesamte Code auch überschaubarer.
Gleichseitiges Dreieck
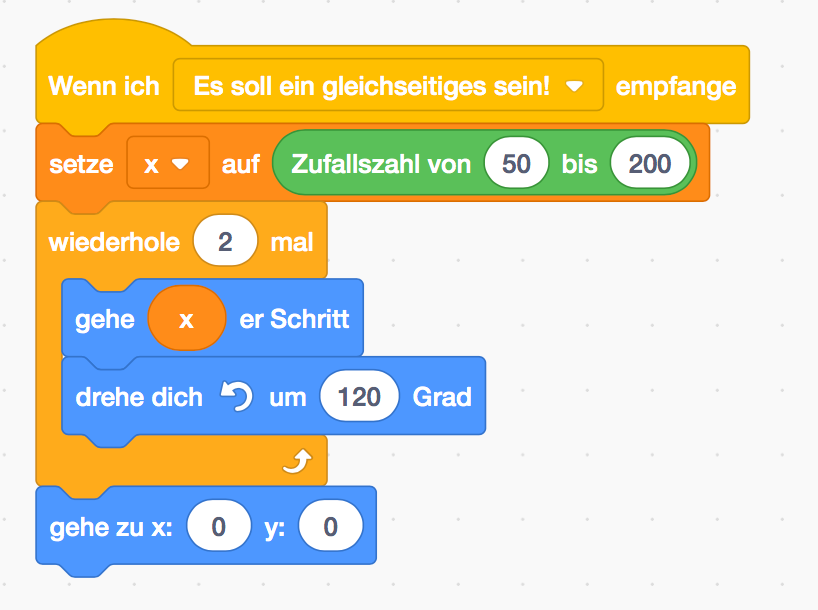
Wichtig ist, dass alle Seiten gleich lang sind und die Winkel jeweils 60 Grad groß sind.
Wie lang die Seiten sind, soll zufällig sein („50 bis 200“ wurde deshalb gewählt, weil das
Dreieck dann eine angenehme Größe bekommt). Die drei Seiten sollen jedoch alle die
gleiche Zufallszahl als Länge haben, weshalb die Variable x auf den Wert gesetzt wird.
Die Drehung um 120 Grad ist nötig, damit die Figur (also der Punkt/Stiftspitze) nicht gerade
geht (entspricht 0 Grad Drehung oder 360 Grad Drehung), nicht zurückgeht (entspricht 180 Grad Drehung), sondern so geht, dass ein Winkel von 60 Grad eingeschlossen wird, also 120(180-60) Grad.
Da es, vor allem, wenn das Dreieck den Rand berührt, passieren kann, dass der Abschluss
nicht exakt ist, wird (anstatt die Schleife einfach 3 Mal zu wiederholen) die dritte Seite
gezeichnet, indem zum Startpunkt zurückgegangen wird.
Rechtwinkliges Dreieck
Wichtig ist, dass ein Winkel 90 Grad groß ist.
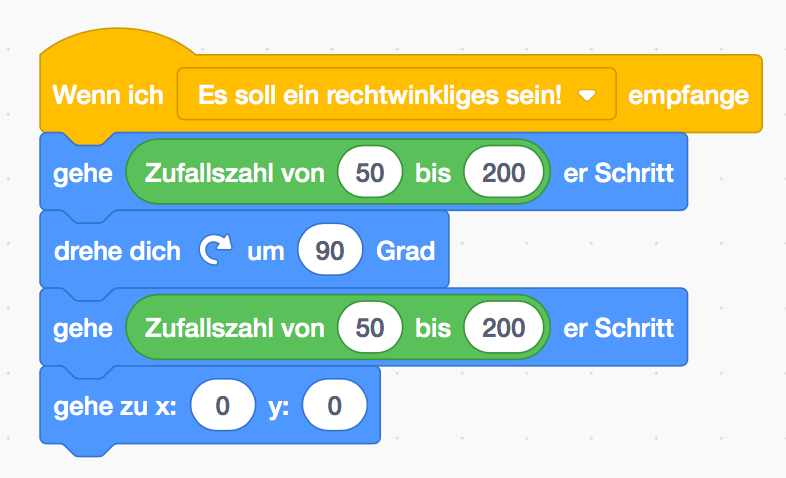
Wie lang die Seiten sind, soll zufällig sein („50 bis 200“ wurde deshalb gewählt, weil das
Dreieck dann eine angenehme Größe bekommt).
Durch die Drehung um 90 Grad, entsteht ein 90 Grad Winkel zwischen den beiden Geraden.
Da die Längen der Seiten diesmal nicht gleich sein müssen, wird ein zweites Mal eine
Zufallszahl gewählt.
Damit der Abschluss exakt ist, wird die dritte Seite gezeichnet, indem zum Startpunkt
zurückgegangen wird.
Da zweimal eine Zufallszahl generiert wird, kann diese Zahl jedoch auch gleich sein und ein
gleichschenkliges Dreieck würde entstehen. (Siehe Zusatzaufgabe 1)
Gleichschenkliges Dreieck
Wichtig ist, dass 2 Seiten gleich lang sind.
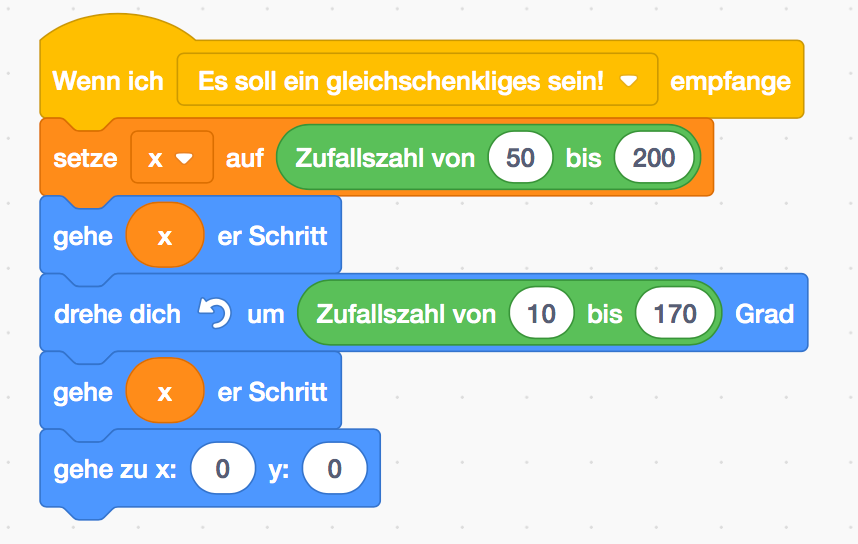
Wie lang die Seiten sind, soll zufällig sein („50 bis 200“ wurde deshalb gewählt, weil das
Dreieck dann eine angenehme Größe bekommt). Zwei Seiten sollen jedoch die gleiche
Zufallszahl als Länge haben, weshalb die Variable x auf den Wert gesetzt wird.
Die Größe des Winkels zwischen den zwei Schenkeln ist egal, solange es möglich ist, dass
ein Dreieck entsteht (also größer als 0 Grad und kleiner als 180 Grad). („10 bis 170“ wurde
deshalb gewählt, weil das Dreieck dann ansehnlicher wird als bei „0.1 bis 179.9)
Damit der Abschluss exakt ist, wird die dritte Seite gezeichnet, indem zum Startpunkt
zurückgegangen wird.
Da eine Drehung um 90 Grad und 120 Grad nicht ausgeschlossen wird, kann immer noch
ein rechtwinkliges oder gleichseitiges Dreieck entstehen. (Siehe Zusatzaufgabe 1)
Rechtwinkliges und gleichschenkliges Dreieck
Wichtig ist, dass 2 Seiten gleich lang sind und ein Winkel 90 Grad groß ist.
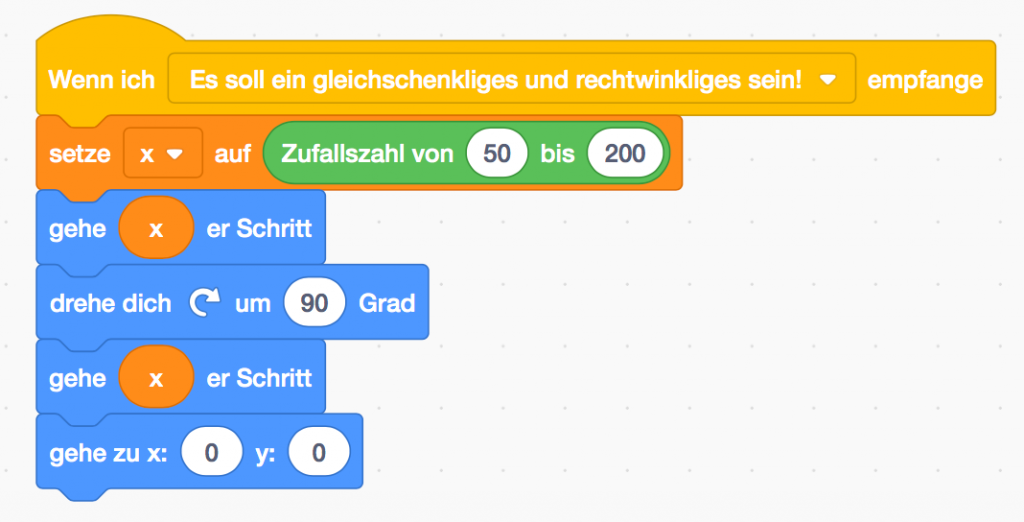
Wie lang die Seiten sind, soll zufällig sein („50 bis 200“ wurde deshalb gewählt, weil das
Dreieck dann eine angenehme Größe bekommt). Zwei Seiten sollen jedoch die gleiche
Zufallszahl als Länge haben, weshalb die Variable x auf den Wert gesetzt wird.
Durch die Drehung um 90 Grad, entsteht ein 90 Grad Winkel zwischen den beiden Geraden.
Damit der Abschluss exakt ist, wird die dritte Seite gezeichnet, indem zum Startpunkt
zurückgegangen wird.
Lösung Zusatzaufgabe 1:
https://scratch.mit.edu/projects/491671540
Rechtwinkliges und nicht gleichschenkliges Dreieck
Wichtig ist, dass ein Winkel 90 Grad groß ist und die zwei Katheten nicht gleich lang sind.
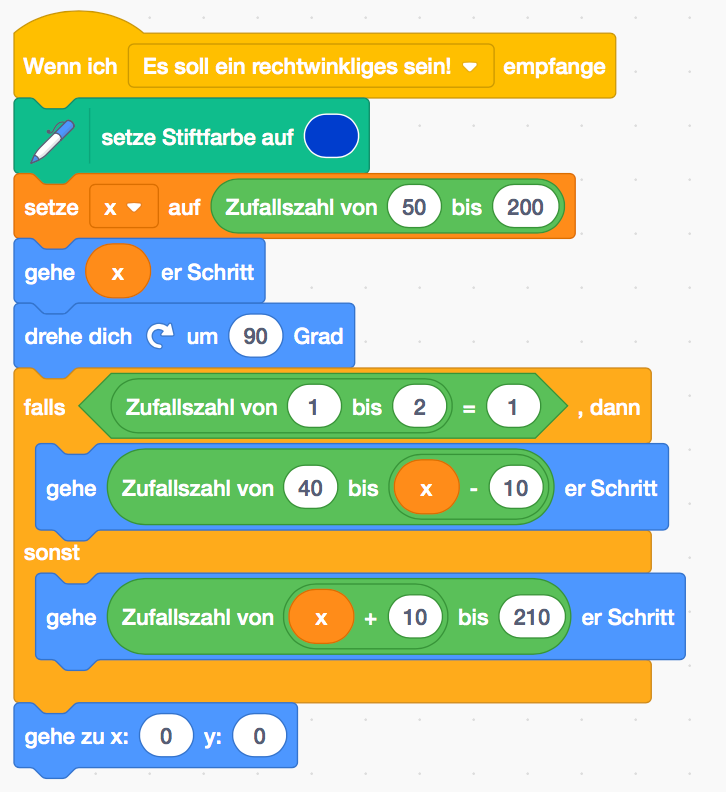
Der Code des rechtwinkligen Dreiecks wird ein wenig abgeändert.
Durch die Zufallszahl 1 bis 2 und die „falls () sonst“ Steuerung wird zu 50% eine Zufallszahl
größer als die Seite x und zu 50% eine Zufallszahl kleiner als die Seite x als Seitenlänge
festgelegt. (Das ist natürlich nicht ganz fair, da x nicht der Median ist.) Zur besseren
Erkennbarkeit wurden auch Werte im Bereich +/- 10 um den Wert x ausgeschlossen. Die
Zufallszahlen wurden mit einem Minimum von 40 und einem Maximum von 210 versehen,
falls der Fall eintritt, dass x genau 50 oder 200 ist.
Gleichschenkliges, nicht rechtwinkliges und nicht gleichseitiges Dreieck
Wichtig ist, dass 2 Seiten gleich lang sind, kein Winkel 90 Grad groß ist und kein Winkel 60
Grad groß ist.
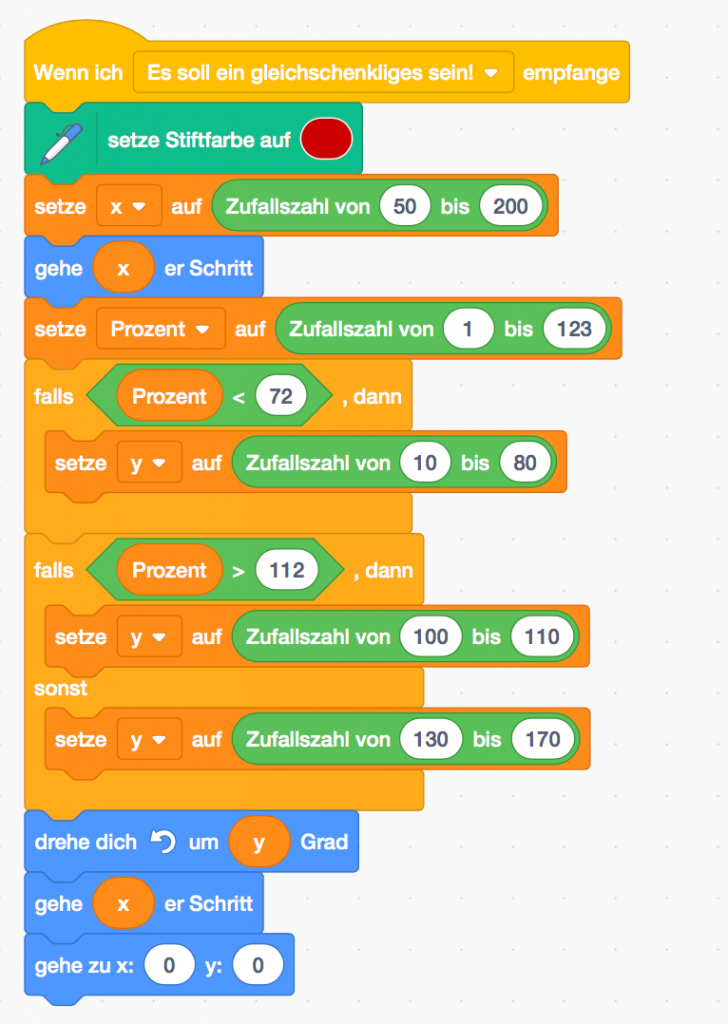
Der Code des gleichschenkligen Dreiecks wird ein wenig abgeändert.
Folgende Werte soll der Winkel zwischen den Schenkeln nicht annehmen: 0, 60, 90, 180.
Also darf die Drehung nicht um folgende Werte erfolgen: 180, 90 120, 0
Zur besseren Erkennbarkeit wurden auch Werte im Bereich +/- 10 um diese Werte
ausgeschlossen.
Für jeden möglichen natürlichen Wert für die Grad soll die gleiche Wahrscheinlichkeit
zugeschrieben sein. Es gibt 123 mögliche Werte. Durch das Ziehen der Zufallszahl von 10 bis 80, wird aus 71 Werten entschieden. Somit soll in 71 (<72) der 123 Fälle aus diesem Intervall gewählt werden. 11 mögliche Zahlen gibt es bei der Zufallszahl von 100 bis 110, somit soll bei 11 (>112) der 123 möglichen Werte aus jenem Intervall gewählt werden. In
den restlichen Fällen, also wenn die Variable „Prozent“ einen der 41 Werte 72, 73, ……. 111,
112 annimmt, soll einer der 41 möglichen Werte der Zufallszahl von 130 bis 170 gewählt
werden.
Lösung Zusatzaufgabe 2:
https://scratch.mit.edu/projects/492232937
Für das Quiz, in dem ein Dreieck erscheint, dem zugeordnet werden soll welches der 4
Dreiecke es ist und Punkte gesammelt werden können, wurde der erste Block verändert,
die Codes für die jeweiligen Dreiecke sind unverändert.
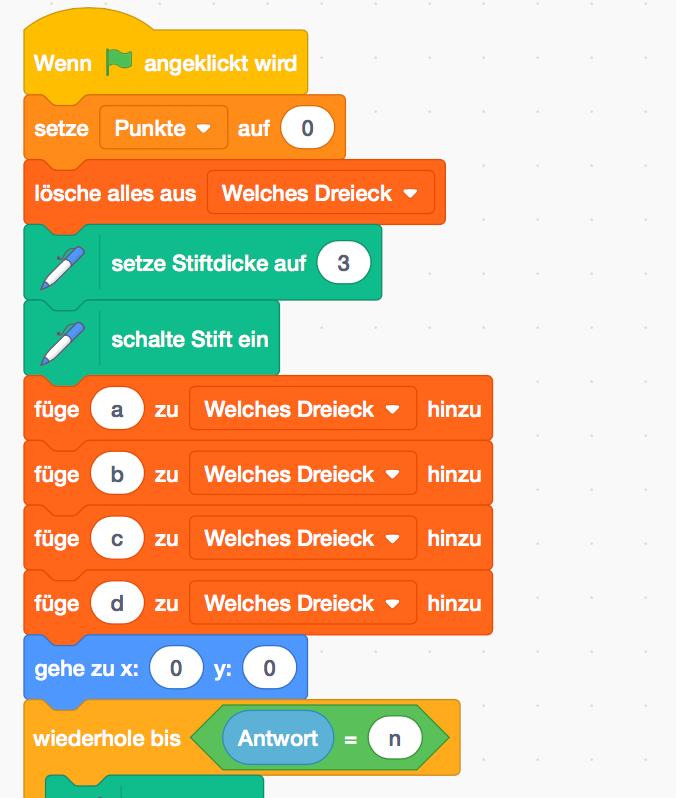
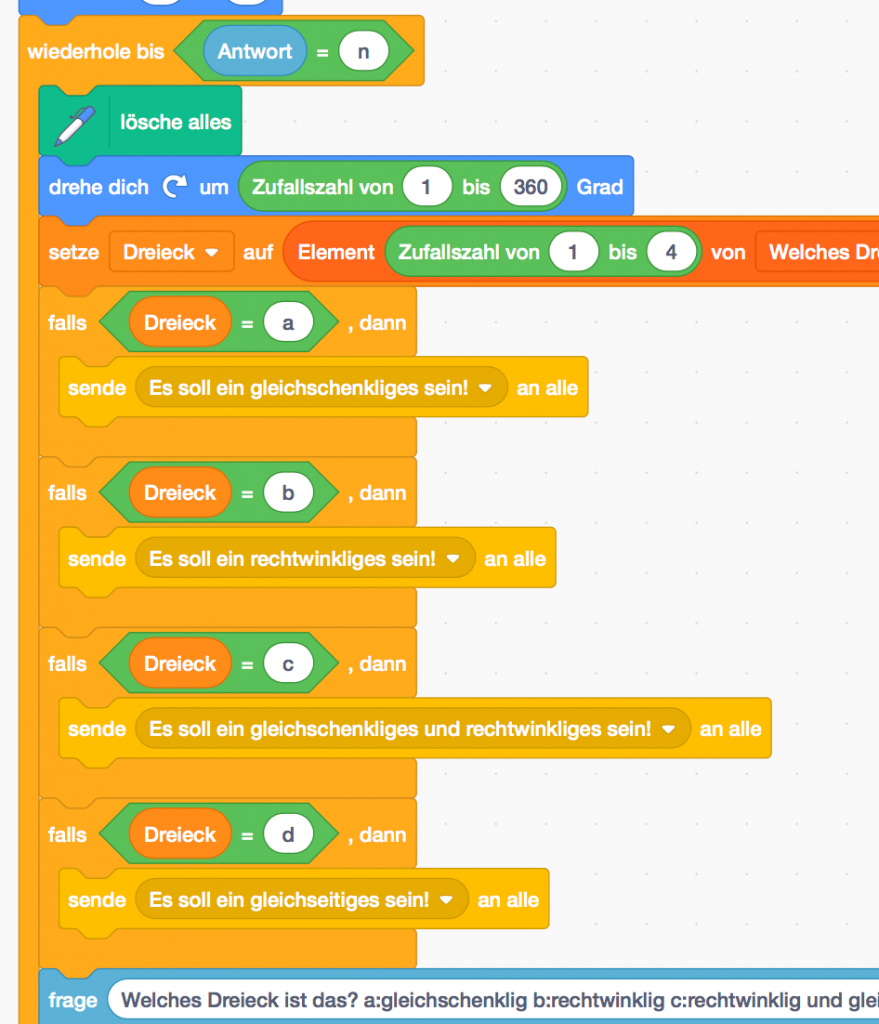
Eine Liste wird angelegt.
Aus dieser wird zufällig ein Element (Dreiecksart) gewählt, der Variablen „Dreieck“
zugeordnet und durch das Senden der Nachricht der Code-Teil für das Zeichnen des
entsprechenden Dreiecks aktiviert.
Dann wird der/die Benutzer*in gefragt, welches Dreieck es ist. Stimmt die Antwort mit der
Variable überein, wird der Punktestand um 1 erhöht. Außerdem wird abgefragt, ob man
noch einmal spielen möchte und die Schleife wird wiederholt bis die Antwort n(ein) lautet.
