EIS Karten Scratch
Hier finden Sie mehrere Aufgabenkarten zu Scratch für den Unterricht. Auf allen Karten befindet sich auch ein QR Code zur Lösung und zu weiteren Informationen.
„EIS Karten Scratch“ weiterlesen
Allgemeines zu Scratch
Scratch ist eine visuelle Programmiersprache, sie wurde von der Lifelong Kindergarten Group am MIT entwickelt. Viele neuere erziehungsorientierte Programmiersprachen nehmen sich das Design von Scratch als Vorbild (Snap!, Ozoblockly, Touchdevelop). „Allgemeines zu Scratch“ weiterlesen
#1 Jump and Run Spiele
Wie der Name schon sagt, steht beim MakeyMakey das Selbermachen im Vordergrund.
Der MakeyMakey ist aus technischer Sicht ein Tastaturersatz an Stelle der Standardtastatur können die einzelnen Tasten dann Bananen, Äpfel, Plastilin, Alufolie oder Personen sein. Die Platine ist ein vereinfachter Arduino, Treiber sind nicht nötig. Auf der Vorderseite finden sich die sechs typischen Spielcontrollertasten, auf der Rückseite zusätzlich Anschlüsse mit der Belegung W, A, S, D, F, den Maustasten und Bewegungstasten. Der Einstieg erfolgt meist mit vorgegebenen Beispielen, die anschließend abgewandelt werden und schließlich Ideengeber für eigene Kreationen sein können.

Jump and Run: für diese Spiele genügt es, wenn für die Pfeilschaltflächen und für die Leertaste jeweils ein Stück Alufolie verwendet wird und mit dem MakeyMakey verbunden wird.
Super Mario: https://scratch.mit.edu/projects/31583772/
Flappy Bird: https://scratch.mit.edu/projects/38729886/
Pacman: https://scratch.mit.edu/projects/14608394/
Spannender wird es, wenn die Spiele mit mehreren Personen gespielt werden und jede/r für eine Taste zuständig ist. Die Felder können auch am Boden ausgelegt werden und man spielt mit den Füßen. Statt Alufolie geht beispielsweise auch Plastilin.



#2 Ein Obstklavier
Wir kombinieren den MakeyMakey und Scratch. Für Tasten können alle stromleitenden Materialien verwendet werden, also auch Äpfel, Bananen usw. so kann man sich bspw. eine einfache Klaviatur aus Bananen bauen.

In Scratch genügt es, wenn die einzelnen Tasten mit jeweils einem Ton belegt werden. Dazu muss man die Erweiterung Musik in Scratch aktivieren.
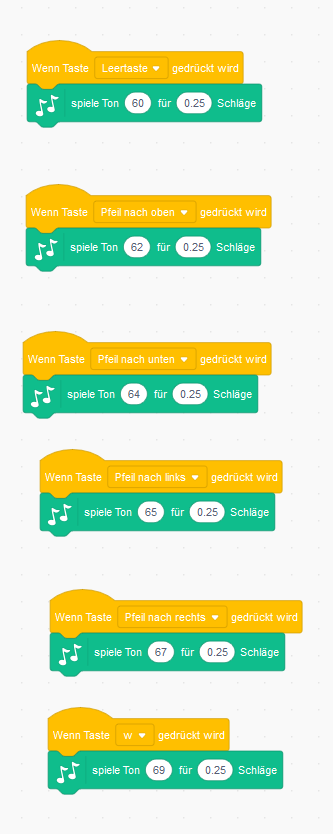
Hier kann man dann auch mit Soundeffekten, selbst aufgenommenen Klängen und Schlagzeugeffekten experimentieren.

#5 Heißer Draht
Dieses Geschicklichkeitsspiel kennst du bestimmt! Dafür benötigst du einen Parcours, diesen kannst du aus Alufolie oder mit einem Draht bauen. Dann brauchst du eine Schlaufe, die durch den Parcours bewegt werden soll. Schließlich ist noch ein Start- und ein Zieltaster vonnöten. Die Schlaufe verkabelst du mit der Erde, die restlichen Teile mit jeweils einer Taste.


So könnte der Code in Scratch aussehen:
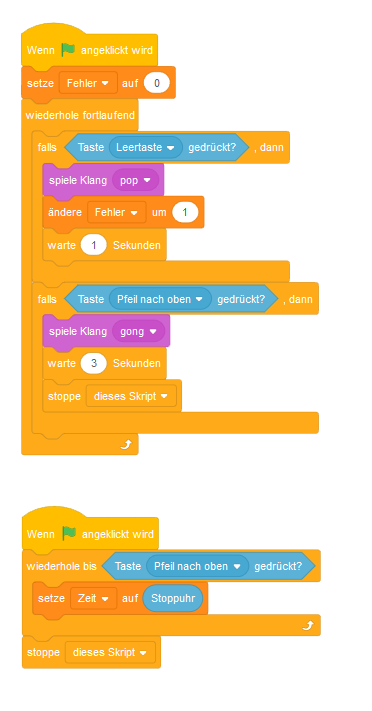

#01 Blume aus überlappenden Kreisen
Ein Projekt von Markus Kautz, für Scratch und Python.
Lösung Scratch:
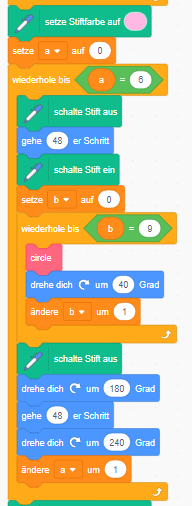
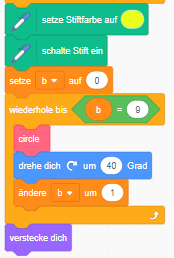
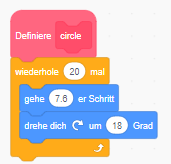
Diese Aufgabe lässt sich mit der Erweiterung „Malstift“ lösen. Für eine einfache Kreisformation kannst du den „Wiederholen bis“-Block aus dem Bereich Steuerung nutzen:
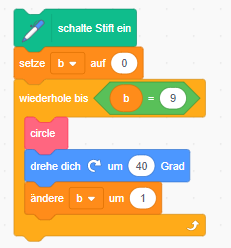
Zeichne die Blume am besten von außen nach innen. Überlege, welche Winkel du dazu
benötigst und an welche Position du den Stift schiebst. Vergiss nicht, beim Bewegen den
Stift zu deaktivieren.
In der Beispiellösung wird der Stift nach dem Zeichnen jeder Kreisformation in die Mitte
zurückbewegt.
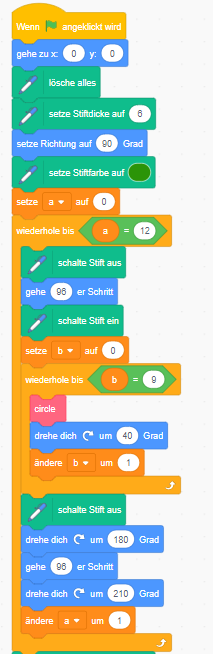
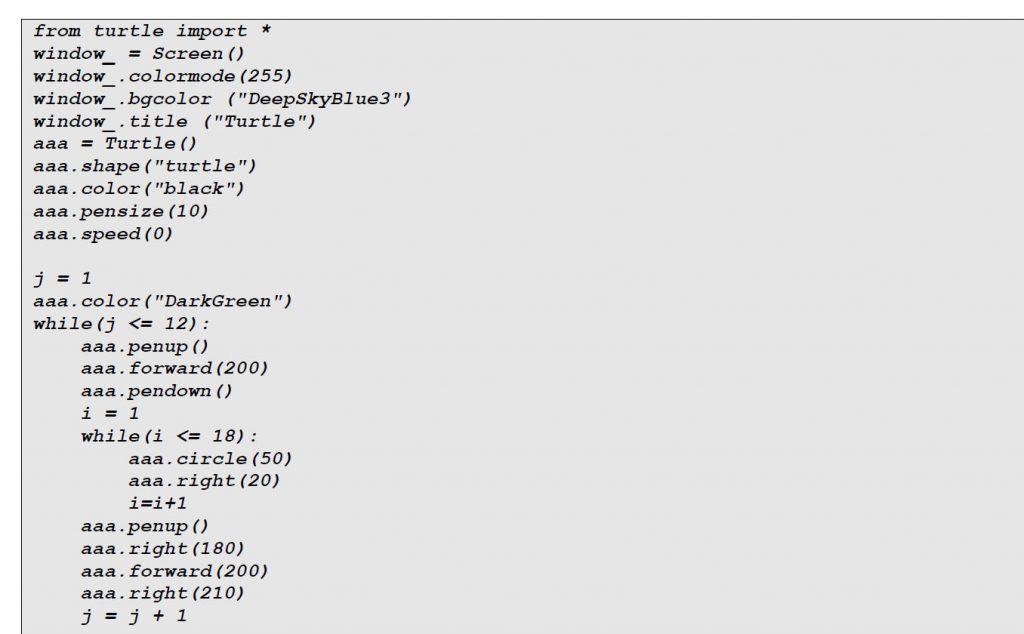
Lösung Python:
Zeichne die Blume am besten von außen nach innen. In der Beispiellösung wurden Kreise
mit Radius 50 verwendet. Achte darauf, die Abstände an deine gewählte Kreisgröße
anzupassen. Die Farben wurden mit tk-color-strings angegeben. Du kannst aber auch
RGB Werte verwenden und so zum Beispiel mit „randint“ Zufallsfarben erzeugen.

#20 Mein Labyrinth
Ein Projekt von David Tran.
Link zur Lösung: https://scratch.mit.edu/projects/505719565/
Um dein persönliches Labyrinth zu zeichnen, kannst du unten rechts auf „Bühnenbilder“ klicken. Oben links kannst du dann im Reiter „Bühnenbilder“ dein eigenes Labyrinth zeichnen.
Code der Figur:
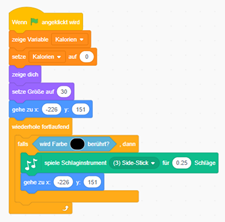
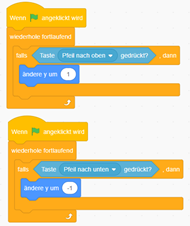
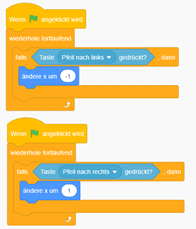
Der Code des Ziels:
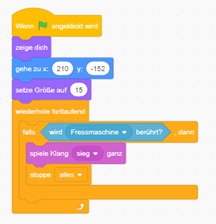
Der Code einer Belohnung:
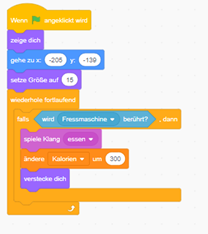
Erweiterung:
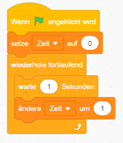
#19 Balloonhunt
Ein Projekt von Elieser Grill.
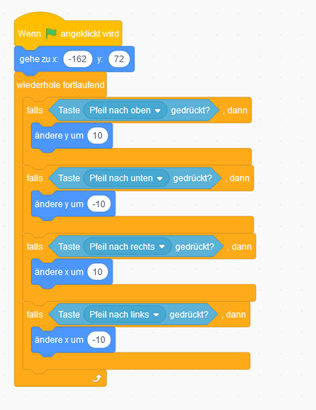
Zu Beginn machen wir die Steuerung für unseren Zauberstab. Mit dem ersten Befehl legst du die Startposition fest. Danach folgen Befehle, mit denen wir die Pfeiltasten so programmieren, dass wir damit den Zauberstab steuern können.
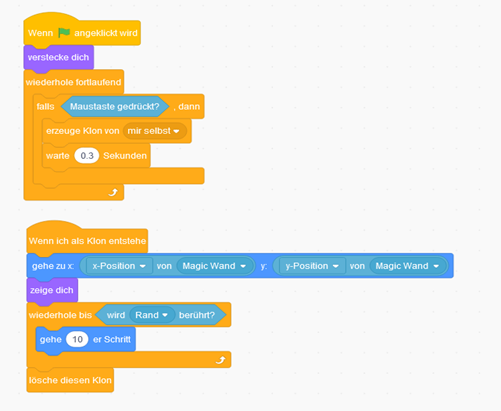
Als Nächstes befassen wir uns mit dem Stern, der unser Projektil darstellt. Der erste Befehl sorgt dafür, dass der Stern zu Beginn nicht sichtbar ist. Dann legen wir fest, dass der Stern, sobald die Maustaste gedrückt wird, einen Klon von sich selbst erzeugt.
Nun folgt der Teil, der festlegt, dass der Stern nicht auf der Stelle bleibt. Sobald ein Klon entsteht, legen wir dessen Startposition fest. Damit es so aussieht, als würden die Sterne aus dem Stab kommen, legen wir als Position des Sterns die des Zauberstabes fest. Danach sorgen wir mit dem Befehl „gehe x- er Schritte“ dafür, dass sich der Stern bewegt. Um zu bewerkstelligen, dass diese Bewegung bis zum anderen Bildschirmrand gemacht wird, packen wir um den Schritte-Befehl eine Schleife herum, die als Bedingung „wird Rand berührt“ hat. Sobald dies der Fall ist, soll der Stern verschwinden, daher auch der „Lösche diesen Klon“-Befehl.
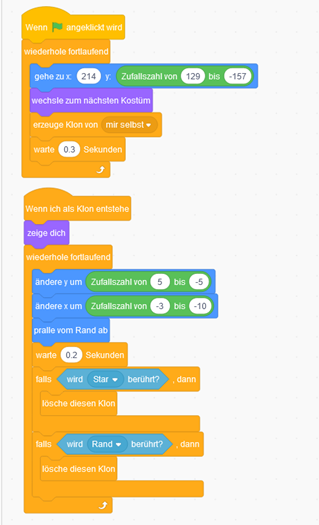
Der letzte Schritt sind die Ballons. Zu Beginn legen wir eine Startposition am rechten Rand fest. Damit der Ballon nicht immer die gleiche Farbe hat, wechseln wir im nächsten Schritt das Kostüm. Anschließend erzeugen wir einen Klon.
Sobald ein Ballon entsteht, müssen wir wie beim Stern dafür sorgen, dass er sich über den Bildschirm bewegt. Hier kommen ein weiteres Mal eine Schleife und Zufallszahlen zum Einsatz. Die Zufallszahlen sollten dabei in einem kleinen Bereich liegen, da dieser Bereich die Größe der Schritte, die ein Ballon macht, festlegt. Um die Geschwindigkeit, mit der sich die Ballons fortbewegen, etwas zu drosseln, fügen wir auch hier einen Wartebefehl ein. Abschließend fehlen nur noch die Bedingungen, die die Ballons zum Verschwinden bringen. Unsere Bedingungen sind in diesem Fall, die Berührung des Sterns oder die des Randes.
Besipielprojekt: https://scratch.mit.edu/projects/505300129/
#17 Im Blumengarten
Ein Projekt von Bernhard Abfalter.
Der Link zur Lösung: https://scratch.mit.edu/projects/505248229/editor
